Asymmetric Diffusion
Edwards B, Camacho M, Engheta N. “Achieving Asymmetry and trapping in diffusion with spatiotemporal metamaterials” Nature Communications (11), 1-7, 2020.
Introduction
Diffusion is the natural consequence of random motion. Between the diffusion equation and the wave equation, the majority of the physics we experience in our daily lives can be explained. Both thermodynamics and electrostatics can be explained as diffusion-based systems.
Similar to waves, in most systems, diffusion is both reciprocal and symmetric. A thermos is equally good at keeping a hot drink warm as it is keeping a cold drink cool. It is very strange when we encounter a system in which diffusion appears to be asymmetric. Without careful analysis, such devices appear dangerously close to perpetual motion machines.
In this work, we created a metamaterial system in which diffusion was not symmetric. Diffusion is based on two quantities: capacity and conductance. We found that by sinusoidally varying these properties with time, we could create systems that were governed by the convection-diffusion equation. In other words, while the material of interest (charge or heat) would diffuse, it would also behave as if it were being blown by a wind, potentially even accumulating at the edge of the system.
By itself, accumulation is surprising as we expect things to spread out in a diffusive system. However, given the sinusoidal undulation of the material parameters, we could imagine that, somehow, that material wants to flow in the direction of the underlying wave. However, the physics gets stranger because the direction of the apparent breeze does not depend on the direction of the undulation. Instead, it depends on the phase difference between how we vary the capacity and conductance of the material. In other words, the wave motion can be moving to the left while the material is moving to the right.
Theory
Standard Diffusion
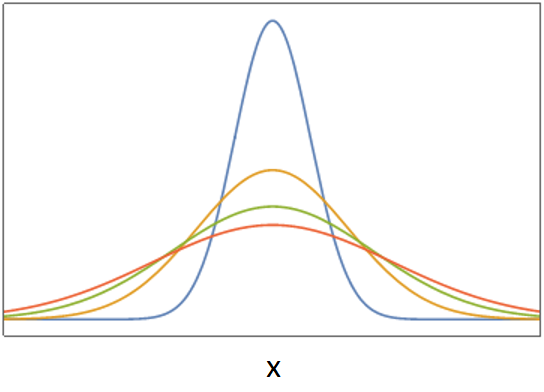
Evolution of a quantity distribution under normal diffusion.
Diffusion can be understood in terms of conservation principles and Fick’s laws of diffusion. This can apply to any conserved quantity such as mass, charge, or a chemical species. We begin the the Conservation Equation:
$$\partial_t Q = -\nabla\cdot\mathbf{J}$$
where $Q$ is the amount of the conserved quantity at a given location and $\mathbf{J}$ is the flux. Put less mathematical terms, this states that the rate a quantity accumulates in a location is related to the flow rate into that location.
We then consider Fick's 1st law:
$$\mathbf{J} = -\sigma\nabla V = -\sigma \nabla(g Q)$$
where $\sigma$ is the local conductivity of the quantity and $V$ is the local potential. The local potential is related to the local capacity of the material, $C$, and we define $g = 1/C$. Put in less mathematical terms, this states that the quantity flows to even out the potential energy everywhere.
Assuming that both the conducitivy and inverse capacity are uniform, these can be combined into the well known diffusion equation:
$$\partial_t Q = -\nabla \cdot (-\sigma \nabla(g Q)) = \sigma g \partial_{x,x} Q = D \partial_{x,x} Q$$ where $D$ is the diffusion coefficient
And this has solutions in the form:
$$ Q(x,t) = \frac{1}{\sqrt{4 \pi D t}}\exp\left(\frac{-x^2}{4 D t}\right)$$
Asymmetric Diffusion
But what if the local conductivity and inverse capacity are not homogeneous and static? What if we modulate them in time and space?
The previous equation can be expanded out to form
$$\partial_t Q = -\nabla \cdot (-\sigma \nabla(g Q))$$ $$\partial_t Q = g \sigma (\partial_{x,x} Q) + (2 (\partial_x g)\sigma + g (\partial_x \sigma)(\partial_x Q) + ((\partial_x g)(\partial_x \sigma) + (\partial_{x,x}g) \sigma))Q$$
This is now much closer to the Advection-Diffusion Equation
$$ \partial_t Q = D \partial_{x,x} Q - v \partial_x Q $$
and this has solutions in the form
$$ Q(x,t) = \frac{1}{\sqrt{4 \pi D t}}\exp\left(\frac{-(x - v t)^2}{4 D t}\right)$$
While the material is diffusing, it is being "blown" in a direction at the velocity $v$.
Equivalent Material Parameters
So now let us suppose that we can modulate the conductivity and inverse capacitance of the the medium. For simplicity, we'll assume that the modulation has the form:
$$ \sigma(x,t) \equiv \sigma_0 + \sigma_a \sin(k x - \omega t)$$ $$ g(x,t) \equiv g_0 + g_a \sin(k x - \omega t + \gamma)$$
The idea is that both $\sigma_a \ll \sigma_0$ and $g_a \ll g_0$. We can imagine this as a small, fast pertubation on top of the larger material parameters.
We then break the solution up into a slow part response with a fast modulation.
$$Q(x,t) \approx \Theta(x,t)(1 + M(x,t))$$
where $\Theta(x,t)$ is the slow response and $M(x,t)$ is the modulation on top of this.
After expanding everything out and canceling small terms, we find that the slow response obeys the equation
$$\partial_t \Theta = g_a \sigma_a \cos(\gamma)/2 + g_0 \sigma_0)\partial_{x,x}\Theta + (g_a \sigma_a k/2) \partial_x\Theta$$
from this we can deduce that the effective diffusion and velocity terms become:
$$ D = g_0 \sigma_0 + \frac{1}{2}g_a \sigma_a \cos(\gamma)$$
$$ v = \frac{1}{2}k g_a \sigma_a sin(\gamma)/2$$
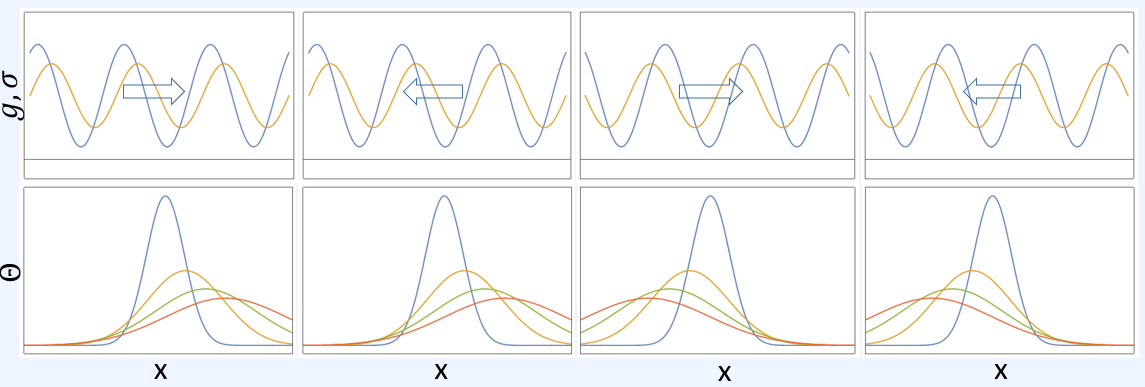
The diffusion term is as we might expect. It will be dominated by $g_0 \sigma_0$. However, the velocity term has some interesting features. First, it does not involve the temporal frequency $\omega$. Second, it is dependent on the relative phase between the material parameters. This means that the effective flow can be opposite of the modulation direction.
The top row shows the relative phase between the conductivity and inverse-capacity of the medium along with the propagation direction of the modulation. The bottom row show the evolution of the quantity distribution. The flow direction is given the spatial offset between the material parameters, not the flow direction.
Experimental Efforts
Inspiration for our device, the rotary variable capacitor (link).
Originally, we had hoped to demonstrate these effects using thermodynamics, but controlling the heat capacity for a material is difficult, making a thermal demonstration challenging.
As a demonstration, we chose electrostatics as the diffusion-based system. Charge is a conserved quantity. Making a variable capacitor is relatively straightforward. We took our inspiration from commercial rotary variable capacitors.
Similarly, a variable conductivity can be created through a series of switches. When the switch is “on” the conductivity for that location is high while when it is “off,” the conductivity is low.
Experimental Design
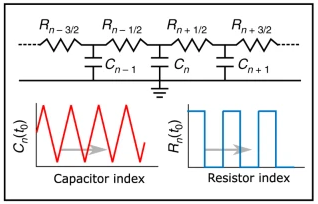
Depiction of the local capacitance and resistance of the system.
In contrast to the standard variable capacitor, each rotor disk was electrically isolated. The rotors were fabricated such that each consisted of a half-metalized plate. When the metalized plate was fully immersed in the stator assembly, the capacitance was high and when it was retracted, the capacitance was low. Each rotor plate was 30deg rotated from the previous, creating a spiral-like arrangement. The portion of the plates immersed in the stator represented a region of high capacitance.
An armature of metallic contacts could bridge the plates. Two neighboring plates were in electrical contact if they were in the range of their rotation in which the contact bridged the metalized portions. Given the spiral-like configuration, this only occurred across a portion of the plates at any given moment, representing a region of high conductivity. The armature could be fixed at different angles to create a phase offset, γ, between the regions of high capacitance and the regions of high conductivity.
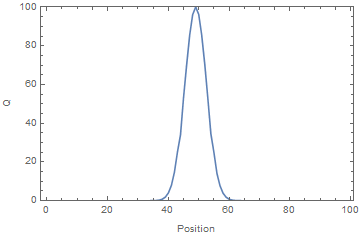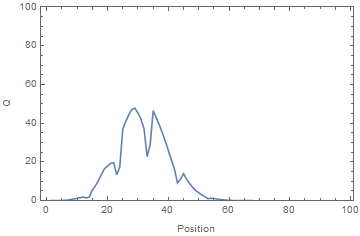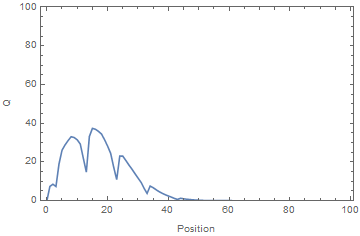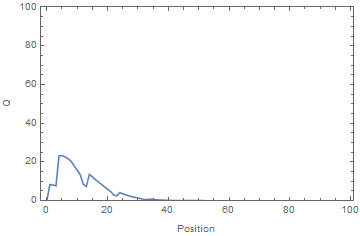
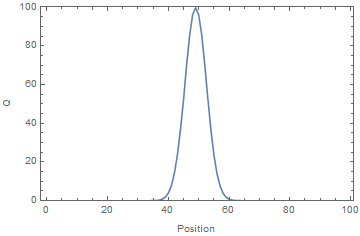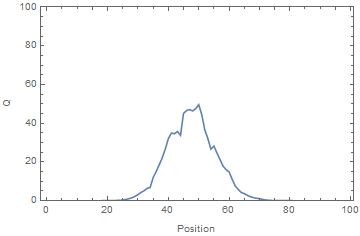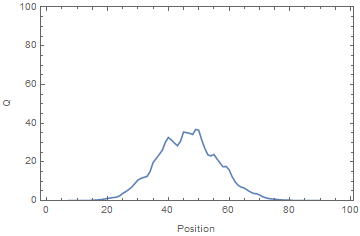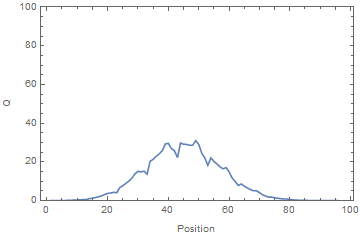
An electrometer, a high impedance DMM, was used to measure the voltage on a subset of the rotor plates. The time-average voltage was used as a proxy for the time-average charge. A voltage source was applied to one end of the system. It can be seen from the results panel below, the charge accumulated at the open (i.e. unconnected) end of the system, where the apparent velocity, v, blew it.
Simulation vs Experiment showing the time evolution of charge (equivalent to voltage) for the system. Note that the charge accumulates at the open (unconnected) end of the system, creating voltages far exceeding that of the source.
Below I show some animations regarding the flow of charge under different schemes. The red lines show the conductivity while the green line shows the inverse capacitance. In all cases, the modulation is happening in the forward direction. Note that there is a phase shift in each of the three cases. This phase shift creates three very different behaviors.