Edwards B, Estakhri NM, Engheta N. "Inverse-designed metastructures that solve equations" Science 363 (6433), 1333-1338, 2019.
Camacho M, Edwards B, Engheta N. “A single inverse-designed photonic structure that performs parallel computing” Nature Communications 12 (1), 1-7, 2021
Inverse Designed Analog Computing at RF Frequencies
Theory
Passive Devices as Linear Operators
The scattering parameters is one way of representing an RF system. Suppose that we consider the system at a single frequency and designate some number of incoming port modes as “input” and an equal number outgoing modes as “output.” Each of the input ports will have a complex amplitude. Taken together, we may consider them a vector $\mathbf{u_\mathrm{in}}$. We will similarly consider the output amplitudes to be $\mathbf{u_\mathrm{out}}$. Due to the linearity of a passive RF system, it follows that the system performs the operation $\mathbf{v} = \mathbf{K} \mathbf{u}$, where $\mathbf{K}$ is a complex matrix. In short, any linear passive RF system can be thought of as performing matrix multiplication.
Solving Systems of Equations
As described above, the system represents a linear operator. A vector of complex amplitudes goes in and a vector of complex amplitudes goes out. We're going to do a relatively simple thing. We're going to loop the system back on itself.
Let's trace the results while taking some liberties with regards to coupling coefficients. Let's denote the vector right before the structure as $\mathbf{u}$. The output of the structure will be $\mathbf{K}\times\mathbf{u}$. We're going to use a coupler to add that to that an input vector $-\mathbf{v}$ to yield $\mathbf{K}\times\mathbf{u} - \mathbf{v}$ and apply that to the input. However, we've already denoted the input to the structure as $\mathbf{u}$. By looping the structure, we've created a linear system of equations that must be obeyed at steady-state.
$$ \mathbf{u} = \mathbf{K}\times\mathbf{u} - \mathbf{v}$$
We can solve this for $\mathbf{u}$ to yield:
$$\mathbf{u} = (\mathbf{K} - \mathbf{I})^{-1} \mathbf{v}$$
where $\mathbf{I}$ is the identity matrix.
This system will compute the inverse of the matrix $(\mathbf{K} - \mathbf{I})$ at optical speeds. In order to probe the results, we can use $\mathbf{v}$. For instance, by illuminate with $\mathbf{v} = [1, 0, ...]$ we can read the first column of the inverted matrix.
How Traditional Design Fails
While any simple passive system with multiple ports can be easily represented by a scattering matrix, it is not trivial to design a structure which achieves the scattering matrix of your choosing. Obviously the chosen scattering matrix must be passive so that energy is conserved. However, even with a theoretically achievable design, it can still be challenging.
For instance, consider a 10-port system. The complex scattering matrix would contain 200 different values of real-valued goal parameters. To set them, you would need at least 200 design parameters. Standard optimization is performed by computing the Jacobian. If we liken optimization to "walking downhill" toward the error minimum, the Jacobian represents the downhill direction in 200-dimensional space. Traditionally, we would compute the Jacobian by doing 200 simulations of the structure, varying each design parameter in turn. We would note whether each change helped (or hurt) our design to achieve the desired scattering matrix. These results would be combined to represent step-direction. We would alter the design by taking a step toward a better design by changing each of the 200 design parameters slightly according to that step-direction. This process would then repeat. Clearly, the bottleneck here is computing the Jacobian. Performing 200 simulations of the structure takes a long time, and this process needs to be repeated for each design step. Additionally, there is no guarantee that the desired matrix is achievable with the 200 design parameters you have chosen. In other words, the chosen scattering matrix might not be in the space of achievable scattering matrices, given the adjustable design parameters.
Inverse Design
However, recently the field of Inverse Design has begun to make powerful advancements with regard to RF and optical system design. For our pet problem, the Jacobian for any number of design parameters can be computed with just 10 simulations. This would be done by illuminating each of the 10 ports in turn. By clever processing of the resulting 10 complex fields, we can determine how to perturb any number of design parameters.
The mathematics behind this are beyond the scope of this webpage. However, I intuitively imagine this as being similar to holography. By interfering a laser with the reversed (phase conjugated) field of the desired image, we can determine the complicated pattern of photoresist which will create that image. If we imagine that photoresist surface as pixelated, this is conceivably millions of design parameters. In simulation, this would be only two simulations to inform a whole 2D space worth of design parameters.
In inverse design, we even give our system more capability than a traditional holographic system by giving our "photoresist" depth. This allows for the resist to interact with itself to form complicated resonant structures and overlapping pathways for the field. We pay a small price for this however. Rather than "developing" the resist in just one iteration, we must allow it to change character slowly over a few hundred iterations. This gives it time to develop these complex structures. There are some holes in this metaphor, but I hope it gives the sense that this isn’t magic.
For further reading on this, useful terms are Automatic Differentiation and the Adjoint Method.
Reflective Experiments
In our first paper (Science 2019) on this topic, we combined these two ideas inverse design and solving systems of linear equations.
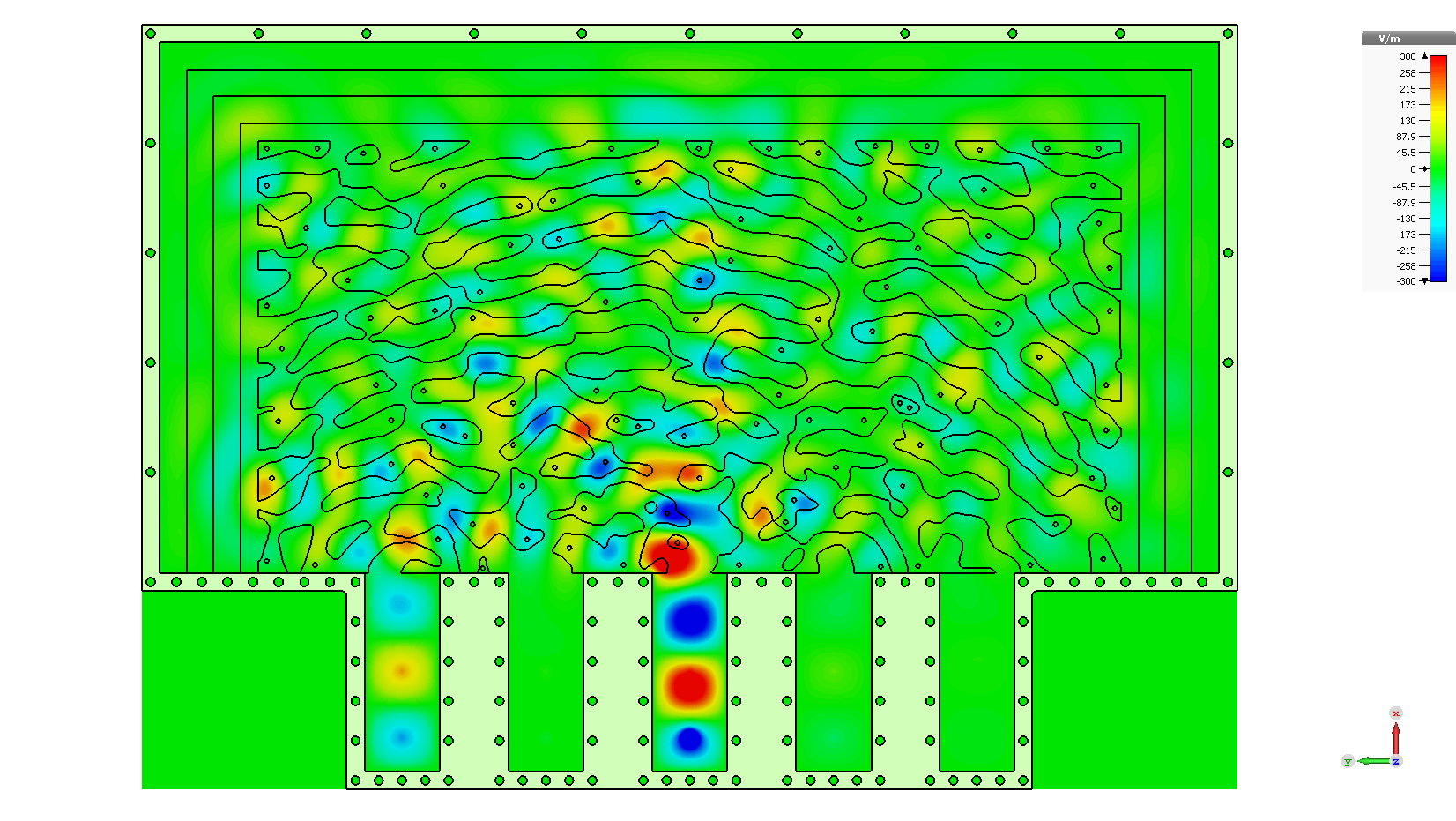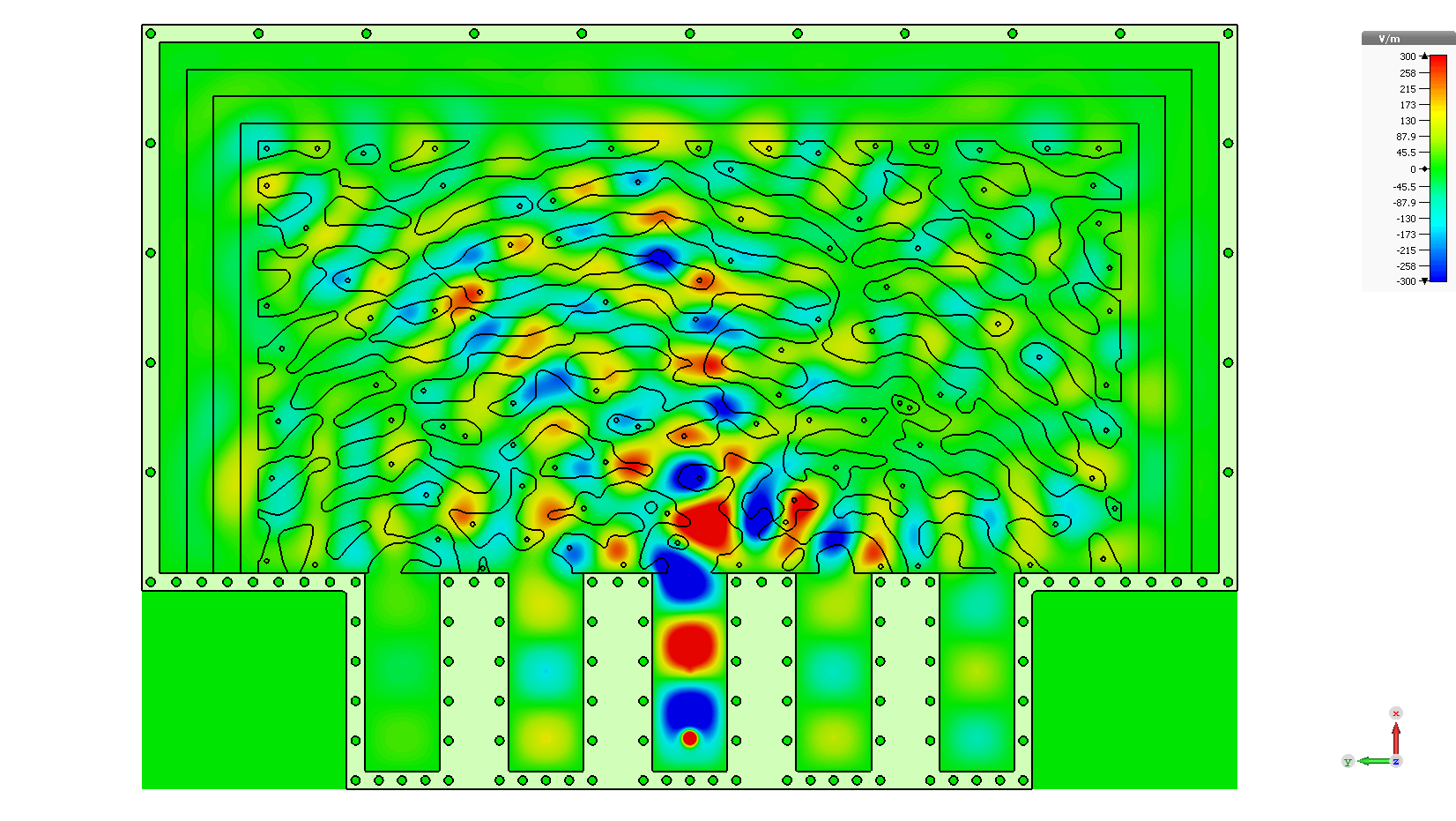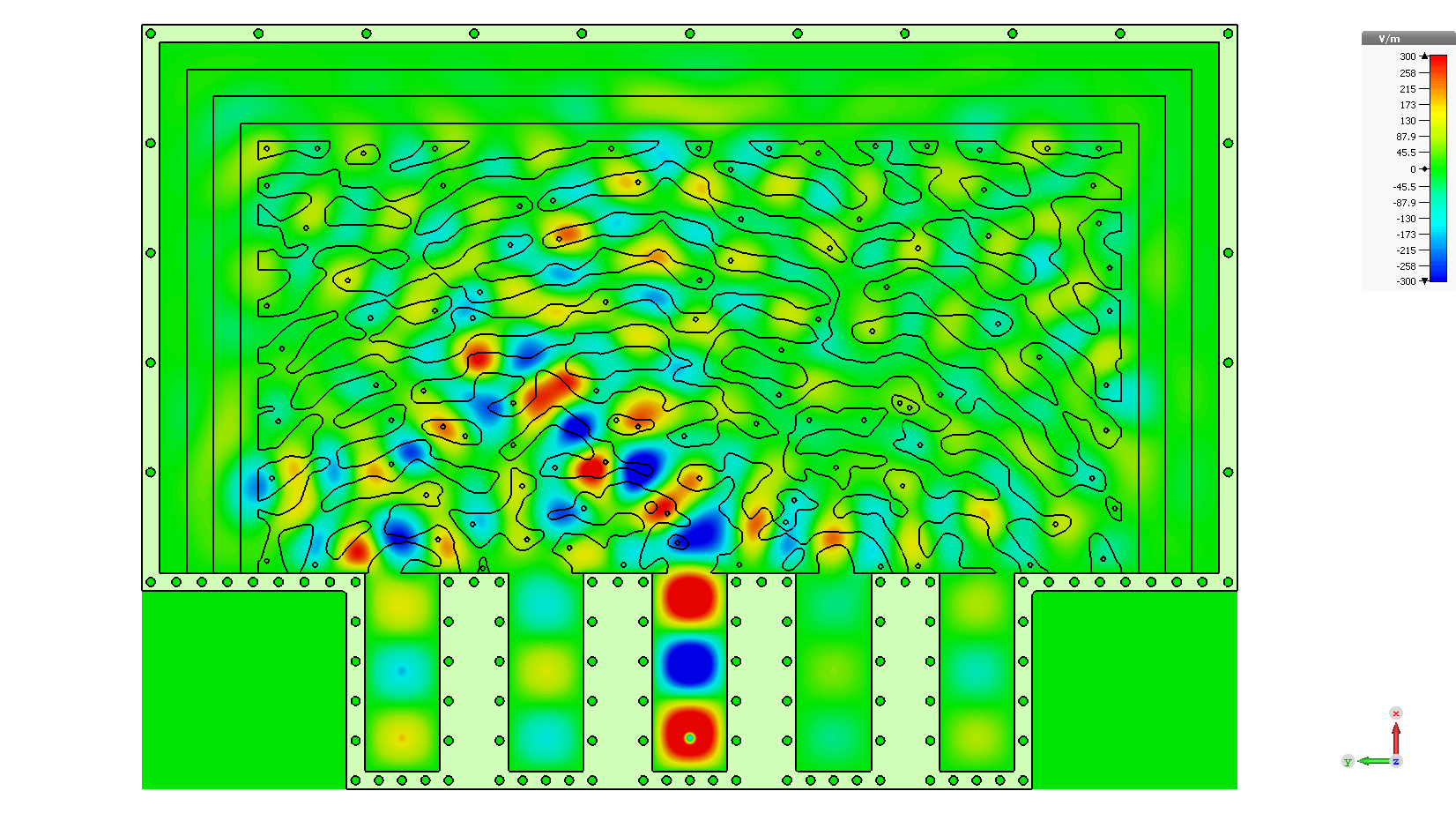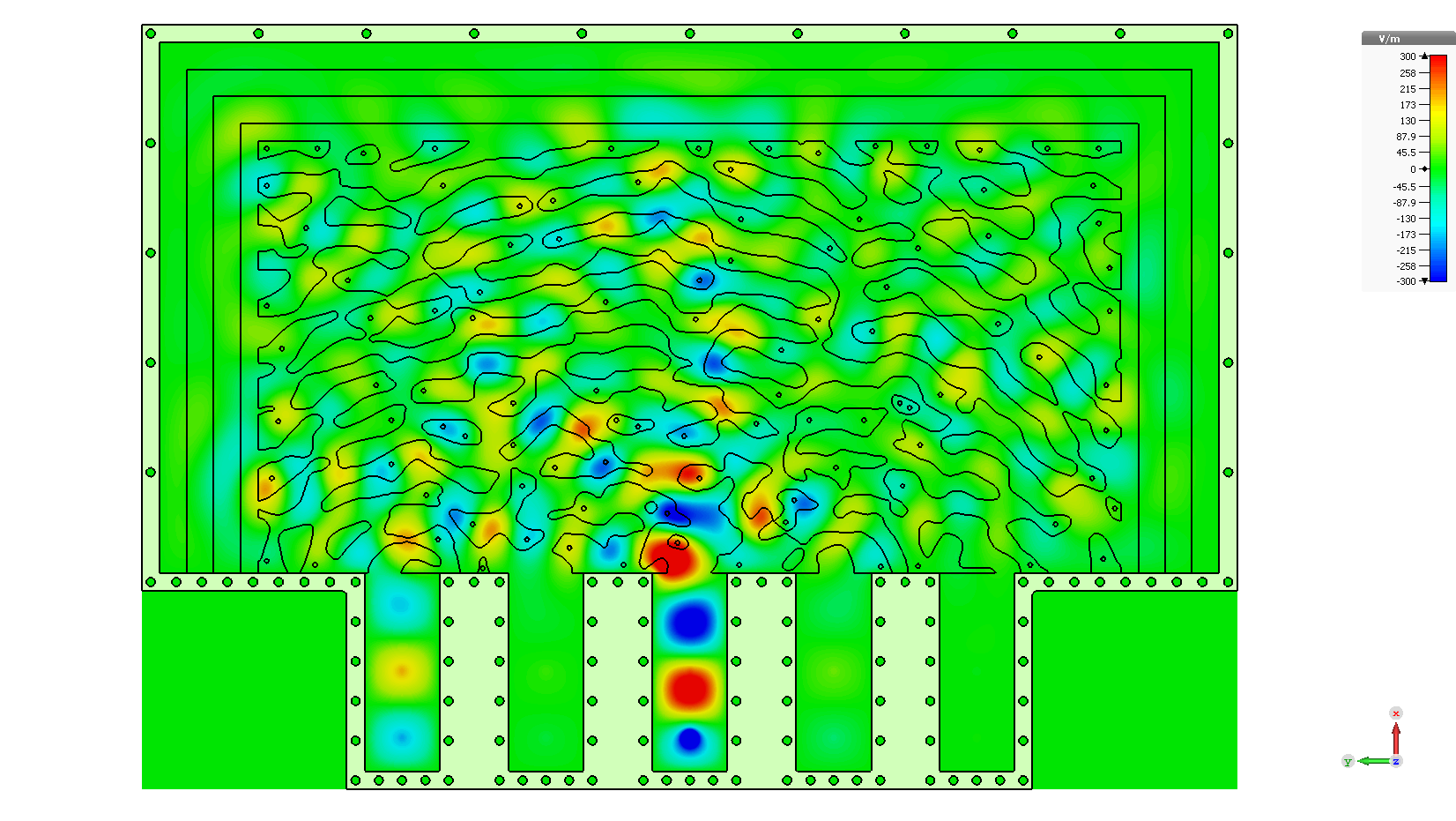
In this experiment, we looked at a reflective kernel. By this, I mean the input modes and the output modes made use of the same physical waveguides. This was done to alleviate the challenges of routing five waveguides around the system with equal path length. Rather, we could simply reflect the output waves back into the kernel. Our chosen kernel must be symmetric because $S_{i,j} = S_{j,i}$. In other words, the transmission from one waveguide to another must be equal regardless of direction.
Within each waveguide, we have two coaxial probes. Both are intentionally poorly coupled to the system. The one closest to the reflecting wall was used to illuminate the waveguide. The other was used measure the wave in each waveguide. The body of the structure was machined out of aluminum, and RF-absorbing foam was used on the perimeter.
The kernel was inverse designed to achieve a desired matrix operation. At this point, commercial software packages such as COMSOL and Lumerical were just beginning to release tools for topological optimization and they didn’t have all the capabilities we needed. I followed the work of Jesse Lu’s doctoral thesis on “Objective First Optimization.” I found this conceptually simpler than automatic differentiation and the adjoint method techniques. However, it requires that you have access to the system matrix that a commercial frequency domain software would solve. I was able to do this in Mathematica by coding my own Finite Difference Frequency Domain (FDFD) solver. Such a system is determined, meaning that it has as many equations as unknowns. However, in order to perform the objective first optimization, you can add additional constraints on the fields regarding both the incoming and outgoing waves at the ports. This makes the overconstrained and unsolvable, but the error can be minimized. The resulting fields will only approximately satisfy Maxwell’s equations. There is information in this deviation, and they can be used to determine the step in permittivity necessary to more closely achieve the design objectives. Doing this all from first principles was a major undertaking, and I don’t recommend it now that commercial solvers exist. The final parts were commerically CNC milled out of a low-loss polystyrene.
Transmissive Experiments
At this point, I took on an advisory role on the project, and my colleague Miguel Camacho took the lead, resulting in our Nature Comms (2021) paper.
We tackled the problem of transmissive kernels by routing the signal under the structure through five PEC rectangular waveguides. Coupling was done with slots. This made it possible to have equal-length waveguides, but introduced some risk with regards to dispersion and achieving the desired round-trip phase.
We needed to illuminate the waveguides in only the forward direction, requiring us to use two coaxial probes to cancel the backward wave. Similarly, we wanted to measure only the forward traveling waves, requiring a two-probe detection scheme.
Finally, we explored the capabilities of inverse design by designing the system to work at two different frequencies for two different kernels.
In this work, the inverse design was performed using COMSOL’s RF and Optimization modules.